Dr. V.K.Maheshwari, M.A(Socio, Phil) B.Sc. M. Ed, Ph.D
Former Principal, K.L.D.A.V.(P.G) College, Roorkee, India
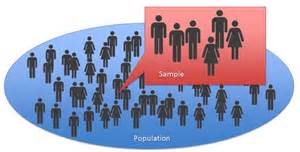
When we are interested in a population, we typically study a sample of that population rather than attempt to study the whole population The purpose of sampling techniques is to help you select units to be included in your sample.
Broadly speaking, there are two groups of sampling technique: probability sampling techniques and non-probability sampling techniques.
Probability sampling techniques
Probability sampling techniques use random selection to help you select units from your sampling frame to be included in your sample. These procedures are very clearly defined, making it easy to follow them.
In probability Samples, each member of the population has a known non-zero probability of being selected. Probability methods include random sampling, systematic sampling, and stratified sampling. Probability sampling includes simple random sampling, systematic sampling, stratified sampling, cluster sampling and disproportional sampling The advantage of probability sampling is that sampling error can be calculated.
In probability sampling, every individual in the population have equal chance of being selected as a subject for the research.
This method guarantees that the selection process is completely randomized and without bias.
The most basic example of probability sampling is listing all the names of the individuals in the population in separate pieces of paper, and then drawing a number of papers one by one from the complete collection of names.
The advantage of using probability sampling is the accuracy of the statistical methods after the experiment. It can also be used to estimate the population parameters since it is representative of the entire population. It is also a reliable method to eliminate sampling bias.
These types of probability sampling technique include simple random sampling, systematic random sampling, stratified random sampling and cluster sampling.
Random sampling
-The random sample is the purest form of probability sampling. Each member of the population has an equal and known chance of being selected. When there are very large populations, it is often difficult or impossible to identify every member of the population, so the pool of available subjects becomes biased.
This may be the most important type of sample. A random sample allows a known probability that each elementary unit will be chosen. This is the type of sampling that is used in lotteries and raffles.
Types of random Samples
A Simple Random Sample-A simple random sample is obtained by choosing elementary units in search a way that each unit in the population has an equal chance of being selected. A simple random sample is free from sampling bias. However, using a random number table to choose the elementary units can be cumbersome. If the sample is to be collected by a person untrained in statistics, then instructions may be misinterpreted and selections may be made improperly.
A systematic random sample-Systematic sampling is often used instead of random sampling. It is also called an Nth name selection technique. After the required sample size has been calculated, every Nth record is selected from a list of population members. As long as the list does not contain any hidden order, this sampling method is as good as the random sampling method. Its only advantage over the random sampling technique is simplicity. Systematic sampling is frequently used to select a specified number of records from a computer file
A systematic random sample is obtained by selecting one unit on a random basis and choosing additional elementary units at evenly spaced intervals until the desired number of units is obtained.
Concept of Randomization
Contrary to popular opinion, samples are not selected haphazardly. Rather they are chosen in a systematically random way so that chance or the operation of probability is utilized. Where random selection is not possible, other systematic means are used.
Randomization is a sampling method used in scientific experiments. It is commonly used in randomized controlled trials in experimental research.
The concept of randomness has been basic to scientific observation and research. It is based on the assumption that while individual events cannot be predicted with accuracy, aggregate events can. For instance, although it may not predict with great accuracy an individual’s academic achievement, it will predict accurately the average academic performance of a group.
In randomized controlled trials, the research participants are assigned by chance, rather than by choice, to either the experimental group or the control group.
Randomization reduces bias as much as possible. Randomization is designed to “control” (reduce or eliminate if possible) bias by all means.
The fundamental goal of randomization is to certain that each treatment is equally likely to be assigned to any given experimental unit.
Randomization has two important applications in research:
1. Selecting a group of individuals for observation who are representative of the population about which the researcher wishes to generalize, or
2. Equating experimental and control groups in an experiment. Assigning individuals by random assignment (each individual in the sample has an equal and independent chance of being assigned to each of the groups) is the best method of providing for their equivalence.
Randomization- Actually Working
Well, there are different options used by researchers to perform randomization. It can be achieved by use of random number tables given in most statistical textbooks or computers can also be used to generate random numbers for us.
If neither of these available, you can devise your own plan to perform randomization. For example, you can select the last digit of phone numbers given in a telephone directory. For example you have different varieties of rice grown in10 total small plots in a greenhouse and you want to evaluate certain fertilizer on 9 varieties of rice plants keeping one plot as a control.
You can number each of the small plots up to 9 and then you can use series of numbers like 8 6 3 1 6 2 9 3 5 6 7 5 5 3 1 and so on
You can then allocate each of three doses of fertilizer treatment (call them doses A, B, C). Now you can apply dose A to plot number 8, B to 6, and C to 3. Then you apply dose A to 1, B to 2 because dose B is already used on plot 6 and so on.
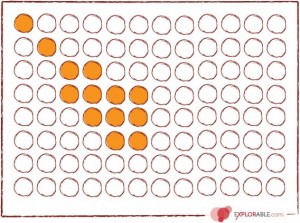
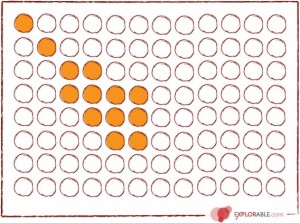
A Stratified Sample-Stratified sampling is commonly used probability method that is superior to random sampling because it reduces sampling error. A stratum is a subset of the population that share at least one common characteristic. . The researcher first identifies the relevant stratums and their actual representation in the population. Random sampling is then used to select a sufficient number of subjects from each stratum. “Sufficient” refers to a sample size large enough for us to be reasonably confident that the stratum represents the population. Stratified sampling is often used when one or more of the stratums in the population have a low incidence relative to the other stratums.
A stratified sample is obtained by independently selecting a separate simple random sample from each population stratum. A population can be divided into different groups may be based on some characteristic or variable .
Stratified sampling is a probability sampling technique wherein the researcher divides the entire population into different subgroups or strata, then randomly selects the final subjects proportionally from the different strata.
Stratified random sampling is a method of sampling that involves the division of a population into smaller groups known as strata. In stratified random sampling, the strata are formed based on members’ shared attributes or characteristics. A random sample from each stratum is taken in a number proportional to the stratum’s size when compared to the population. These subsets of the strata are then pooled to form a random sample.
The main advantage with stratified sampling is how it captures key population characteristics in the sample. Similar to a weighted average, this method of sampling produces characteristics in the sample that are proportional to the overall population. Stratified sampling works well for populations with a variety of attributes, but is otherwise ineffective, as subgroups cannot be formed.
It is important to note that a random sample is not necessarily an identical representation of the population. Characteristics of successive random samples drawn from the same population may differ to some degree, but it is possible to estimate their variation from the population characteristics and from each other. The variation, known as sampling error, does not suggest that a mistake has been made in the sampling process. Rather, sampling error refers to the chance variations that occur in sampling; with randomization these variations are predictable and taken into account in data-analysis techniques.
It is important to note that the strata must be non-overlapping. Having overlapping subgroups will grant some individuals higher chances of being selected as subject. This completely negates the concept of stratified sampling as a type of probability sampling.
Equally important is the fact that the researcher must use simple probability sampling within the different strata.
The most common strata used in stratified random sampling are age, gender, socioeconomic status, religion, nationality and educational attainment.
Stratified random sampling is used when the researcher wants to highlight a specific subgroup within the population. This technique is useful in such researches because it ensures the presence of the key subgroup within the sample.
Researchers also employ stratified random sampling when they want to observe existing relationships between two or more subgroups. With a simple random sampling technique, the researcher is not sure whether the subgroups that he wants to observe are represented equally or proportionately within the sample.
With stratified sampling, the researcher can representatively sample even the smallest and most inaccessible subgroups in the population. This allows the researcher to sample the rare extremes of the given population.
With this technique, you have a higher statistical precision compared to simple random sampling. This is because the variability within the subgroups is lower compared to the variations when dealing with the entire population.
Because this technique has high statistical precision, it also means that it requires a small sample size which can save a lot of time, money and effort of the researchers.
Types of Stratified Sampling
A-Proportionate Stratified Random Sampling
The sample size of each stratum in this technique is proportionate to the population size of the stratum when viewed against the entire population. This means that the each stratum has the same sampling fraction.
For example, you have 3 strata with 100, 200 and 300 population sizes respectively. And the researcher chose a sampling fraction of ½. Then, the researcher must randomly sample 50, 100 and 150 subjects from each stratum respectively.
Stratum A B C
Population Size 100 200 300
Sampling Fraction ½ ½ ½
Final Sample Size 50 100 150
The important thing to remember in this technique is to use the same sampling fraction for each stratum regardless of the differences in population size of the strata. It is much like assembling a smaller population that is specific to the relative proportions of the subgroups within the population.
B- Disproportionate Stratified Random Sampling
The only difference between proportionate and disproportionate stratified random sampling is their sampling fractions. With disproportionate sampling, the different strata have different sampling fractions.
precision of this design is highly dependent on the sampling fraction allocation of the researcher. If the researcher commits mistakes in allotting sampling fractions, a stratum may either be overrepresented or underrepresented which will result in skewed results.
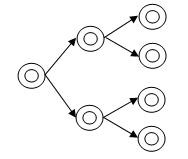
A Cluster Sample
-A cluster sample is obtained by selecting clusters from the population on the basis of simple random sampling. The sample comprises a census of each random cluster selected. Cluster sampling is a method used to enable random sampling to occur while limiting the time and costs that would otherwise be required to sample from either a very large population or one that is geographically diverse. Using this method, a one- or two-level randomization process is used the important element in this process is that each one of the criteria have an equal opportunity to be chosen, with no researcher or facility bias.
The area or cluster sample is a variation of the simple random sample that is particularly appropriate when the population of interest is infinite, when a list of the members of the population does not exist, or when the geographic distribution of the individuals is widely scattered.
Non-probability sampling techniques
In this type of population sampling, members of the population do not have equal chance of being selected. Due to this, it is not safe to assume that the sample fully represents the target population. It is also possible that the researcher deliberately chose the individuals that will participate in the study.
Non-probability sampling techniques refer on the subjective judgement of the researcher when selecting units from the population to be included in the sample. For some of the different types of non-probability sampling technique, the procedures for selecting units to be included in the sample are very clearly defined, just like probability sampling techniques. However, in others (e.g., purposive sampling), the subjective judgement required to select units from the population, which involves a combination of theory, experience and insight from the research process, makes selecting units more complicated. Overall, the types of non-probability sampling technique include quota sampling, purposive sampling, convenience sampling, snowball sampling and self-section sampling.
Non-probability population sampling method is useful for pilot studies, case studies, qualitative research, and for hypothesis development.
Non-Probability Sampling, members are selected from the population in some nonrandom manner. Non-probability sampling includes convenience sampling, consecutive sampling, judgmental sampling, quota sampling and snowball sampling. In non-probability sampling, the degree to which the sample differs from the population remains unknown
Convenience Sampling
In all forms of research, it would be ideal to test the entire population, but in most cases, the population is just too large that it is impossible to include every individual. This is the reason why most researchers rely on sampling techniques like convenience sampling, the most common of all sampling techniques. Many researchers prefer this sampling technique because it is fast, inexpensive, easy and the subjects are readily available.
Convenience sampling is a non-probability sampling technique where subjects are selected because of their convenient accessibility and proximity to the researcher.
The subjects are selected just because they are easiest to recruit for the study and the researcher did not consider selecting subjects that are representative of the entire population.
-Convenience sampling is probably the most commonly used technique in research today . With convenience sampling, subjects are selected because of their convenient accessibility to the researcher. These subjects are chosen simply because they are the easiest to obtain for the study. This technique is easy, fast and usually the least expensive and troublesome convenience sample results when the more convenient elementary units are chosen from a population for observation. Convenience sampling is used in exploratory research where the researcher is interested in getting an inexpensive approximation of the truth. As the name implies, the sample is selected because they are convenient. This Non-probability method is often used during preliminary research efforts to get a gross estimate of the results, without incurring the cost or time required to select a random sample.
Researchers use convenience sampling not just because it is easy to use, but because it also has other research advantages.
In pilot studies, convenience sample is usually used because it allows the researcher to obtain basic data and trends regarding his study without the complications of using a randomized sample.
This sampling technique is also useful in documenting that a particular quality of a substance or phenomenon occurs within a given sample. Such studies are also very useful for detecting relationships among different phenomena.
The most obvious criticism about convenience sampling is sampling bias and that the sample is not representative of the entire population. This may be the biggest disadvantage when using a convenience sample because it leads to more problems and criticisms.
Systematic bias stems from sampling bias. This refers to a constant difference between the results from the sample and the theoretical results from the entire population. It is not rare that the results from a study that uses a convenience sample differ significantly with the results from the entire population. A consequence of having systematic bias is obtaining skewed results.
Another significant criticism about using a convenience sample is the limitation in generalization and inference making about the entire population. Since the sample is not representative of the population, the results of the study cannot speak for the entire population. This results to a low external validity of the study.
When using convenience sampling, it is necessary to describe how your sample would differ from an ideal sample that was randomly selected. It is also necessary to describe the individuals who might be left out during the selection process or the individuals who are overrepresented in the sample.
Consecutive Sampling
Consecutive Sampling is a strict version of convenience sampling where every available subject is selected, i.e., the complete accessible population is studied. This is the best choice of the Non-probability sampling techniques since by studying everybody available, a good representation of the overall population is possible in a reasonable period of time.
Consecutive Sampling is very similar to convenience sampling except that it seeks to include ALL accessible subjects as part of the sample. This non-probability sampling technique can be considered as the best of all non-probability samples because it includes all subjects that are available that makes the sample a better representation of the entire population.
Consecutive sampling is a sampling technique in which every subject meeting the criteria of inclusion is selected until the required sample size is achieved. Consecutive sampling technique involves selecting all individuals who agree to participate, provided they meet pre-extablished criteria, until the number of subjects desired has been recruited. For example, the author of this text once conducted a study of the verbal memory of adult dyslexics who were recruited by means of several techniques including appeals through newspaper and radio advertising. In order to qualify as subjects, several criteria had to be satisfied with respect to age, IQ level, educational achievement, history of remediation, mental and physical status, and scores on standardized tests of reading ability, among other factors. Consecutive sampling can be highly useful when the available subject pool is limited or when using selection criteria so stringent as to reduce the number of subjects to a point that threatens the generality of findings. Although consecutive sampling methods are typically stronger than other nonprobability methods in controlling sampling bias, such confounding influence cannot be ruled out. Response rate, the proportion of the subjects willing to participate of those selected, may also influence the validity of inferences. For instance, subjects who agree to participate may have different motivations or life circumstances than those who do not.
Judgmental sampling
Judgmental sampling is a non-probability sampling technique where the researcher selects units to be sampled based on their knowledge and professional judgment.
The Judgment Sample-Judgmental sampling, also called Purposive Sampling or authoritative sampling , is another form of convenience sampling where subjects are handpicked from the accessible population Subjects usually are selected using judgmental sampling because the researcher believes that certain subjects are likely to benefit or be more compliant A judgement sample is obtained according to the discretion of someone who is familiar with the relevant characteristics of the population. It is a common non-probability method. The researcher selects the sample based on judgment.
The judgemental sampling is used in cases where the specialty of an authority can select a more representative sample that can bring more accurate results than by using other probability sampling techniques. The process involves nothing but purposely handpicking individuals from the population based on the authority’s or the researcher’s knowledge and judgment.
Judgmental sampling design is usually used when a limited number of individuals possess the trait of interest. It is the only viable sampling technique in obtaining information from a very specific group of people. It is also possible to use judgmental sampling if the researcher knows a reliable professional or authority that he thinks is capable of assembling a representative sample.
The two main weaknesses of authoritative sampling are with the authority and in the sampling process; both of which pertains to the reliability and the bias that accompanies the sampling technique.
Unfortunately, there is usually no way to evaluate the reliability of the expert or the authority. The best way to avoid sampling error brought by the expert is to choose the best and most experienced authority in the field of interest.
When it comes to the sampling process, it is usually biased since no randomization was used in obtaining the sample. It is also worth noting that the members of the population did not have equal chances of being selected. The consequence of this is the misrepresentation of the entire population which will then limit generalizations of the results of the study.Purposeful sampling is often used in qualitative research studies.
Quota Sampling-
Quota sampling is the Non-probability equivalent of stratified sampling. Like stratified sampling, the researcher first identifies the stratums and their proportions as they are represented in the population. Then convenience or judgment sampling is used to select the required number of subjects from each stratum. This differs from stratified sampling, where the stratums are filled by random sampling Quota sampling is a non-probability technique used to ensure equal representation of subjects in each layer of a stratified sample grouping.
It is a technique wherein the assembled sample has the same proportions of individuals as the entire population with respect to known characteristics, traits or focused phenomenon.
In addition to this, the researcher must make sure that the composition of the final sample to be used in the study meets the research’s quota criteria.
The first step in non-probability quota sampling is to divide the population into exclusive subgroups.
Then, the researcher must identify the proportions of these subgroups in the population; this same proportion will be applied in the sampling process.
Finally, the researcher selects subjects from the various subgroups while taking into consideration the proportions noted in the previous step.
The final step ensures that the sample is representative of the entire population. It also allows the researcher to study traits and characteristics that are noted for each subgroup.
In a study wherein the researcher likes to compare the academic performance of the different high school class levels, its relationship with gender and socioeconomic status, the researcher first identifies the subgroups.
Usually, the subgroups are the characteristics or variables of the study. The researcher divides the entire population into class levels, intersected with gender and socioeconomic status. Then, he takes note of the proportions of these subgroups in the entire population and then samples each subgroup accordingly.
The main reason why researchers choose quota samples is that it allows the researchers to sample a subgroup that is of great interest to the study. If a study aims to investigate a trait or a characteristic of a certain subgroup, this type of sampling is the ideal technique.
Quota sampling also allows the researchers to observe relationships between subgroups. In some studies, traits of a certain subgroup interact with other traits of another subgroup. In such cases, it is also necessary for the researcher to use this type of sampling technique.
It may appear that this type of sampling technique is totally representative of the population. In some cases it is not. Keep in mind that only the selected traits of the population were taken into account in forming the subgroups.
In the process of sampling these subgroups, other traits in the sample may be overrepresented. In a study that considers gender, socioeconomic status and religion as the basis of the subgroups, the final sample may have skewed representation of age, race, educational attainment, marital status and a lot more.
Sequential Sampling
Sequential sampling is a non-probability sampling technique wherein the researcher picks a single or a group of subjects in a given time interval, conducts his study, analyzes the results then picks another group of subjects if needed and so on.
Sequential sampling technique, initially developed as a tool for product quality control. The sample size, n, is not fixed in advanced, nor is the timeframe of data collection. The process begins, first, with the sampling of a single observation or a group of observations. These are then tested to see whether or not the null hypothesis can be rejected. If the null is not rejected, then another observation or group of observations is sampled and the test is run again. In this way the test continues until the researcher is confident in his or her results.
For survey sampling applications, the term sequential sampling describes any method of sampling that reads an ordered frame of N sampling units and selects the sample with specified probabilities or specified expectations. Sequential sampling methods are particularly well suited when applied with computers. They can also be applied for selecting samples of a population resulting from some other process: for example, cars coming off an assembly line, patients arriving at a clinic, or voters exiting the polls. Examples of sequential sampling schemes discussed in this entry include simple random sampling, systematic sampling, and probability proportional to size (PPS) sequential sampling.
This technique can reduce sampling costs by reducing the number of observations needed. If a whole batch of light bulbs is defective, sequential sampling can allow us to learn this much more quickly and inexpensively than simple random sampling. However, it is not a random sample and has other issues with making statistical inference.
This sampling technique gives the researcher limitless chances of fine tuning his research methods and gaining a vital insight into the study that he is currently pursuing.
If we are to consider all the other sampling techniques in research, we will all come to a conclusion that the experiment and the data analysis will either boil down to accepting the null hypothesis or disproving the null hypothesis while accepting the alternative hypothesis.
In sequential sampling technique, there exists another step, a third option. The researcher can accept the null hypothesis, accept his alternative hypothesis, or select another pool of subjects and conduct the experiment once again. This entails that the researcher can obtain limitless number of subjects before finally making a decision whether to accept his null or alternative hypothesis.
The researcher has a limitless option when it comes to sample size and sampling schedule. The sample size can be relatively small of excessively large depending on the decision making of the researcher. Sampling schedule is also completely dependent to the researcher since a second group of samples can only be obtained after conducting the experiment to the initial group of samples.
As mentioned above, this sampling technique enables the researcher to fine-tune his research methods and results analysis. Due to the repetitive nature of this sampling method, minor changes and adjustments can be done during the initial parts of the study to correct and hone the research method.
There is very little effort in the part of the researcher when performing this sampling technique. It is not expensive, not time consuming and not workforce extensive.
This sampling method is hardly representative of the entire population. Its only hope of approaching representativeness is when the researcher chose to use a very large sample size significant enough to represent a big fraction of the entire population.
The sampling technique is also hardly randomized. This contributes to the very little degree representativeness of the sampling technique.
Due to the aforementioned disadvantages, results from this sampling technique cannot be used to create conclusions and interpretations pertaining to the entire population.
Be sure to understand the limitations of the technique. Sequential modeling is not a probabilistic sampling option. It can lead to valid statistical conclusions but the means in which these are obtained is separate from probabilistic sampling techniques.
Systematic Sampling
Systematic sampling is a random sampling technique which is frequently chosen by researchers for its simplicity and its periodic quality.
Systematic sampling is a type of probability sampling method in which sample members from a larger population are selected according to a random starting point and a fixed periodic interval. This interval, called the sampling interval, is calculated by dividing the population size by the desired sample size. Despite the sample population being selected in advance, systematic sampling is still thought of as being random if the periodic interval is determined beforehand and the starting point is random.
In systematic random sampling, the researcher first randomly picks the first item or subject from the population. Then, the researcher will select each n’th subject from the list.
The procedure involved in systematic random sampling is very easy and can be done manually. The results are representative of the population unless certain characteristics of the population are repeated for every n’th individual, which is highly unlikely.
Since simply random sampling a population can be inefficient and time-consuming, statisticians turn to other methods, such as systematic sampling. Choosing a sample size through a systematic approach can be done quickly. Once a fixed starting point has been identified, a constant interval is selected to facilitate participant selection.
For example, if you wanted to select a random group of 1,000 people from a population of 50,000 using systematic sampling, all of the potential participants must be placed in a list and a starting point would be selected. Once the list is formed, every 50th person on the list, starting the count at the selected starting point, would be chosen as a participant, since 50,000/1,000 = 50. For example, if the selected starting point was 20, the 70th person on the list would be chosen followed by the 120th, and so on. Once the end of the list was reached, if additional participants are required, the count loops to the beginning of the list to finish the count.
Within systematic sampling, as with other sampling methods, a target population must be selected prior to selecting participants. A population can be identified based on any number of desired characteristics that suit the purpose of the study being conducted. Some selection criteria may include age, gender, race, location, education level and/or profession
The process of obtaining the systematic sample is much like an arithmetic progression.
Starting-Number
The researcher selects an integer that must be less than the total number of individuals in the population. This integer will correspond to the first subject.
1-Interval:
The researcher picks another integer which will serve as the constant difference between any two consecutive numbers in the progression.
The integer is typically selected so that the researcher obtains the correct sample size
For example, the researcher has a population total of 100 individuals and need 12 subjects. He first picks his starting number, 5.
Then the researcher picks his interval, 8. The members of his sample will be individuals 5, 13, 21, 29, 37, 45, 53, 61, 69, 77, 85, 93.
Other researchers use a modified systematic random sampling technique wherein they first identify the needed sample size. Then, they divide the total number of the population with the sample size to obtain the sampling fraction. The sampling fraction is then used as the constant difference between subjects.
Risks Associated with Systematic Sampling
One risk that statisticians must take into account when conducting systematic sampling involves how the list used with the sampling interval is organized. If the population placed on the list is organized in a cyclical pattern that matches the sampling interval, the selected sample may be biased. For example, a company’s human resources department wants to pick a sample of employees and ask how they feel about company policies. Employees are grouped in teams of 20, with each team headed by a manager. If the list used to pick the sample size is organized with teams clustered together, the statistician risks picking only managers (or no managers at all) depending on the sampling interval.
Advantage and Disadvantage of systematic sampling
- Another advantage of systematic random sampling over simple random sampling is the assurance that the population will be evenly sampled. There exists a chance in simple random sampling that allows a clustered selection of subjects. This is systematically eliminated in systematic sampling.
- The main advantage of using systematic sampling over simple random sampling is its simplicity. It allows the researcher to add a degree of system or process into the random selection of subjects.
- The process of selection can interact with a hidden periodic trait within the population. If the sampling technique coincides with the periodicity of the trait, the sampling technique will no longer be random and representativeness of the sample is compromised
Since systematic random sampling is a type of probability sampling, the researcher must ensure that all the members of the population have equal chances of being selected as the starting point or the initial subject.
The researcher must be certain that the chosen constant interval between subjects do not reflect a certain pattern of traits present in the population. If a pattern in the population exists and it coincides with the interval set by the researcher, randomness of the sampling technique is compromised.
Snowball or Chain Sampling
This particular one identifies, cases of interest from people who know people who know what cases are information rich that is good examples for study, good interview subjects. This is commonly used in studies that may be looking at issues like the homeless households. What you do is to get hold of one and he/she will tell you where the others are or can be found. When you find those others they will tell you where you can get more others and the chain continues. Snowball sampling is a special Non-probability method used when the desired sample characteristic is rare. It may be extremely difficult or cost prohibitive to locate respondents in these situations. Snowball sampling relies on referrals from initial subjects to generate additional subjects. While this technique can dramatically lower search costs, it comes at the expense of introducing bias because the technique itself reduces the likelihood that the sample will represent a good cross section from the population.
Snowball sampling is a non-probability sampling technique that is used by researchers to identify potential subjects in studies where subjects are hard to locate.
Snowball Sampling
Researchers use this sampling method if the sample for the study is very rare or is limited to a very small subgroup of the population. This type of sampling technique works like chain referral. After observing the initial subject, the researcher asks for assistance from the subject to help identify people with a similar trait of interest.
The process of snowball sampling is much like asking your subjects to nominate another person with the same trait as your next subject. The researcher then observes the nominated subjects and continues in the same way until the obtaining sufficient number of subjects.
For example, if obtaining subjects for a study that wants to observe a rare disease, the researcher may opt to use snowball sampling since it will be difficult to obtain subjects. It is also possible that the patients with the same disease have a support group; being able to observe one of the members as your initial subject will then lead you to more subjects for the study.
Types of Snowball Sampling
- Linear Snowball Sampling
- Exponential Non-Discriminative Snowball Sampling
- Exponential Discriminative Snowball Sampling
Advantages and Disadvantages of Snowball Sampling
- The chain referral process allows the researcher to reach populations that are difficult to sample when using other sampling methods.
- The process is cheap, simple and cost-efficient.
- This sampling technique needs little planning and fewer workforce compared to other sampling techniques.
- The researcher has little control over the sampling method. The subjects that the researcher can obtain rely mainly on the previous subjects that were observed.
- Representativeness of the sample is not guaranteed. The researcher has no idea of the true distribution of the population and of the sample.
- Sampling bias is also a fear of researchers when using this sampling technique. Initial subjects tend to nominate people that they know well. Because of this, it is highly possible that the subjects share the same traits and characteristics, thus, it is possible that the sample that the researcher will obtain is only a small subgroup of the entire population.